Subsequent calculation and evaluation

Command: post_models(“calc_losses”, “L”)

Calculation and evaluation of iron and eddy-current losses in permeable and electrically conductive areas. The “retroactivity” of hysteresis or eddy currents on the field causing them is neglected.

Parameter

[out] L Returns the losses under this (freely selectable) variable identifier.

If a single field calculation has been carried out, the iron-loss calculation is based on the local flux-density in the element, wherein a sinusoidal waveform of flux-density is assumed. In a field calculation with rotation or time-changing current, such as for

  • run_models(“mult_cal_fast”)

  • run_models(“cogg_calc”)

  • run_models(“pm_sym_fast”)

the iron losses are calculated on the basis of the harmonic analysis of the flux-density waveform in the element. In both cases, the Steinmetz and Jordan model is used, as the FEMAG-Handbook explains in more detail.

Parameter definition

The parameters of the loss calculation can be

  • pre_models(“FE-Losses-1/2”)

  • pre_models(“CU-Losses-1/2”)

  • pre_models(“conduct-data”)

  • pre_models(“Magnet-data”)

as described in the section Model and machine parameters, or via direct data access under Machine and Model.

Example

-- m.lossfunct    =      0   -- Iron loss func.: intern=0, script>0     0
   m.coordx       =   44.4   -- Location of loss calculation x   [mm]
   m.coordy       =   38.4   -- Location of loss calculation y   [mm]
   m.frequency    =  100.0   -- Frequency                        [Hz]
-- m.armlength    =   50.0   -- Effective armature length        [mm]   1
-- m.numpolpair   =      2   -- Number of pole pairs           (>= 1)
-- m.npolsgen     =      1   -- Number of poles simulated      (>= 1)
-- m.lossfact     =   1.00   -- Iron loss multipl. factor: 1 .. 1.8     1
-- m.betastep     =      1   -- Current angle:                          0
                             -- 0 = noload, 1 = zero, 2 = as specified
-- m.currentstep  =      1   -- Current step                            1
-- m.maglosscm    =      0   -- Magnet loss calculation method          0
                             -- 0 = J method, 1 = B method

 postmodels(,)

 felosses = L[1]            -- Iron losses   [W]
 pmlosses = L[2]            -- Magnet losses [W]

The parameters annotated with “–” are optional. If they are not specified, the base model parameters BMP (see Model and machine parameters) are used or, if they are also not defined, the value in curly brackets is assumed. The loss values returned in L refer to the selected range and the entire machine (not only the modeled part).

Field Calculation with Motion/Rotation or Time-Changing Currents

The storage of the induction curves in the elements must be carried out via the parameter before the field calculation is activated (see Calculation parameters).

m.calcfeloss = 1            -- Calcul. FE-Loss > 0, areas <0, no = 0

pre_models("FE-contr-data");

Use of own iron loss models

The m.loss_funct parameter allows the loss calculation to be stored as a script function for values greater than 0 to use specific models. The function definition described below is provided.

Function definition for the Jordan model: m.loss_funct = 1 or 2

The function is passed the amplitudes of the partial oscillations Bxnu and Bynu of the components of the induction vector in the x- and y-direction as well as their frequency fnu.

Function definition:

ph, pw, stat = pfe(Bxnu, Bynu, kh, fnu, km, zone, dist)
Parameter
[in] Bxnu Flux-density amplitude; x-component [T]
[in] Bynu Flux-density amplitude; y-component [T]
[in] kh Hysteresis factor (rotating/pulsating)
[in] fnu Frequency [Hz]
[in] km Material factor (Supplement factor “Zuschlagsfaktor”)
[in] zone Stanzkantenzone (1..4)
[in] dist Stanzkantendistanz
[in] km Material factor (Supplement factor “Zuschlagsfaktor”)
[in] zone Stanzkantenzone (1..4)
[in] dist Stanzkantendistanz
[out] ph Hysteresis loss [W/m³]
[out] pw Eddy-current loss [W/m³]
[out] stat Status of the execution (0 = error; 1 = no error)

The function is called for each element and for each partial cycle of the flux-density waveform at the frequency fnu with the orthogonal amplitudes Bxnu and Bynu; and the hysteresis loss density ph and eddy-current loss density pw over the selected subregion (m.coord_x and m.coord_y) are returned. The value of kh depends on the ratio of the main axes of the trajectory of the flux-density vector and its amplitude, thus taking into account the different hysteresis losses in the case of pulsating and rotating fields.

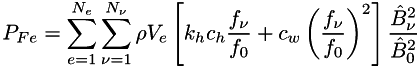
../../../../../../_images/form_16.png

In the case of stat = 0, the iron loss calculation in FEMAG is aborted with an error.

If m.loss_funct = 1, partial variations of flux-density with amplitudes (smaller than 0.08 T) are suppressed; this can also arise due to imperfect periodicity of gradients due to edge effects in the Fourier transformation. If m.loss_funct = 2 no filtering is performed.

Beispiel einer Funktionsdefinition entsprechend dem intern in FEMAG verwendeten Verlustmodell (erweitertes Jordan-Modell)

pfe(Bxnu,Bynu,kh,fnu,km,z,d)

-- Übergebene Argumente:
-- Bxnu Induktionsamplitude x-Komponente [T]
-- Bynu Induktionsamplitude y-Komponente [T]
-- kh   Hysteresefaktor (rotierend/pulsierend)
-- fnu  Frequenz [Hz]
-- km   Materialfaktor (Zuschlagsfaktor)
-- z    Stanzkantenzone
-- d    Stanzkantendistanz

-- **Return value**:
-- ph   Hystereseverluste   [W/m3]
-- pw   Wirbelstromverluste [W/m3]
-- stat Fehlerstatus (0 = Fehler, 1 = ohne Fehler)

-- Modellparameter (auch außerhalb der Funktion definierbar)

basfrq = 50.0     -- Base Frequency  ch and cw [Hz]
basind = 1.5      -- Base Induction (Peak) [T]
ch = 4.0          -- Fe Hysteresis Coefficient   [W/kg]
cw = 2.0          -- Fe Eddy Current Coefficient [W/kg]
hyscoef = 1.0     -- Hysteresis Frequency Coefficient
edycoef = 2.0     -- Eddy Current Frequency Coefficient
indcoef = 2.0     -- Induction Coefficient
spweight = 7.65   -- Specific Weight Iron [gr/cm3]
fillfact = 1.0    -- Fillfactor Iron <= 1

-- Eisenverlustmodell

hxx = Bxnu/fillfact
hyy = Bynu/fillfact
b21 = math.sqrt(hxx*hxx+hyy*hyy)
b2 = math.pow(b21/basind,indcoef)
hi = fnu/basfrq
hch = math.pow(hi,hyscoef)
hcw = math.pow(hi,edycoef)
ph = kh*ch*hch*b2*spweight*1000.0*km
pw = cw*hcw*b2*spweight*1000.0*km

stat = 1
 ph, pw, stat
end

Alternative function definition for using the IEM model [4]: m.loss_funct = 3

This allows more detailed consideration of rotating and pulsating fields. In contrast to the previous model, the minimum value Bmin and the maximum value Bmax of the amplitude of the flux-density vector are transferred to the function and additionally the harmonic order nu of the oscillation, as well as the number of the currently evaluated element. The maximum value can serve as a measure of the degree of saturation and the quotient Bmin/Bmax can be used to distinguish areas with rotating and pulsating fields.

[1] Simon Steentjes, Daniel Eggers, Marc Leßmann and Kay Hameyer, Iron-loss model for the FE-simulation of electrical machines, Institute of Electrical Machines (IEM), RWTH Aachen, In Proceedings of the Inductica Technical Conference, Berlin 2012.

Function definition:

ph, pw, stat = pfe(Bxnu, Bynu, Bmin, Bmax, fnu, nu, elkey, zone, dist)
Parameter
[in] Bxnu Flux-density amplitude; x-component [T]
[in] Bynu Flux-density amplitude; y-component [T]
[in] Bmin Minimum amplitude of the flux-density vector [T]
[in] Bmax Maximum amplitude of the flux-density vector [T]
[in] fnu Frequency of the flux-density variation [Hz]
[in] nu Harmonic order of the flux-density variation
[in] elkey No. of evaluated elements
[in] zone Stanzkantenzone (1..4)
[in] dist Stanzkantendistanz
[out] ph Hysteresis loss [W/m³]
[out] pw Eddy-current loss [W/m³]
[out] stat Status of the execution (0 = error; 1 = no error)

The function is called for each element, and for each minor loop of the flux-density of harmonic order nu and frequency fnu with the orthogonal amplitudes Bxnu and Bynu the hysteresis loss density ph and eddy-current loss density pw are returned for the selected subregion (m.coord_x and m.coord_y).

Example of a function definition:

function pfe(Bxnu, Bynu, Bmin, Bmax, fnu, nu, elkey, zone, dist)

 -- Übergebene Argumente:
 -- Bxnu  Induktionsamplitude x-Komponente [T]
 -- Bynu  Induktionsamplitude y-Komponente [T]
 -- Bmin  Minimalwert des Betrages des Induktionsvektors [T]
 -- Bmax  Maximalwert des Betrages des Induktionsvektors [T]
 -- fnu   Frequenz der Induktionsschwingung [Hz]
 -- nu    Ordnungzahl der Induktionsschwingung
 -- elkey Nummer des ausgewerteten Elements
 -- zone Stanzkantenzone (1..4)
 -- dist Stanzkantendistanz

 -- **Return value**:
 -- ph    Hystereseverluste   [W/m3]
 -- pw    Wirbelstromverluste [W/m3]
 -- stat  Fehlerstatus (0 = Fehler, 1 = ohne Fehler)

 -- ... Eisenverlustberechnung erfolgt hier

 stat = 1
  ph, pw, stat
end

The function is called for each element, and for each minor loop of the flux-density of harmonic order nu and frequency fnu with the orthogonal amplitudes Bxnu and Bynu the hysteresis loss density ph and eddy-current loss density pw are returned for the selected subregion (m.coord_x and m.coord_y).

function colgrad(elkey,val,low,high)    -- user defined   color gradations
  val>=low and val<=high then           -- of quantities
   rval=(val-low)/(high-low)
   col = 45-(45-21)*rval
   draw_elem(elkey,col,0)
  elseif val<low then
   draw_elem(elkey,,0)
  elseif val > high then
   draw_elem(elkey,"black",0)
  end
 return
end

function pfe(Bx,By,Bmin,Bmax,fnu,nu,elkey)

  -- ... iron loss calculation have to be done here

  if nu == 1 then                 -- in case of fundamental flux density
    colgrad(elkey,Bmin/Bmax,0,1)  -- draw elements in color
  end

  stat = 1
  return ph, pw, stats
end

m.loss_func = 3    -- select above function pfe for specific iron loss calculation

post_models("calc_losses","L")
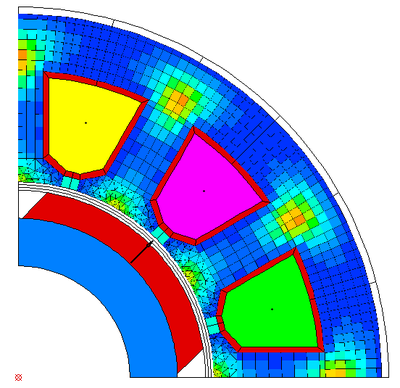
../../../../../../_images/losses_iem_Bmin_by_Bmax.png

After calculating the iron losses in the stator, the quotient Bmin/Bmax is shown in colour gradations. A value of 0 is blue and the value 1 is red. Bright areas, i.e. with Bmin/Bmax approximately 1, are those with predominantly rotating field.

Additional information